Programming

Trees And Graphs

樹的類型 (Types of Trees)

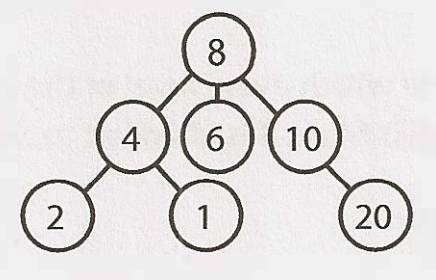
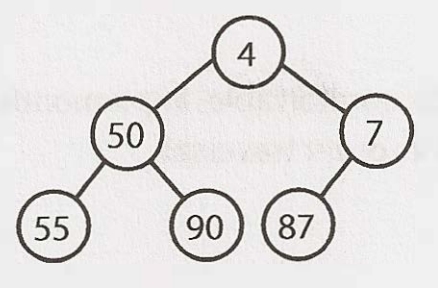
樹與二元樹 (Trees vs. Binary Trees)

指每個節點最多兩個子節點的樹。並非所有的樹是二元樹。

ternary-tree

無子節點的節點稱為葉 (leaf)。

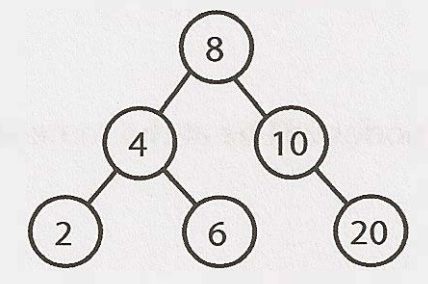
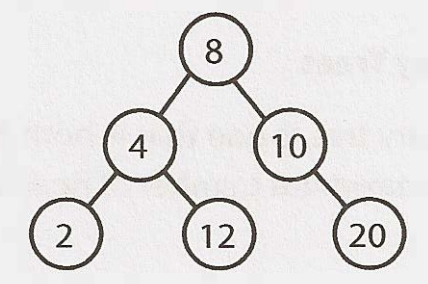
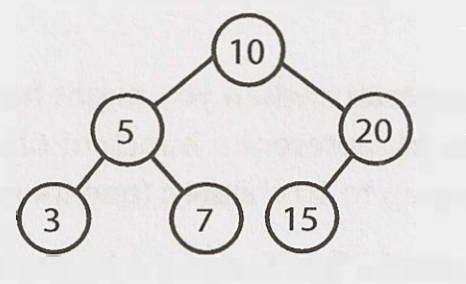
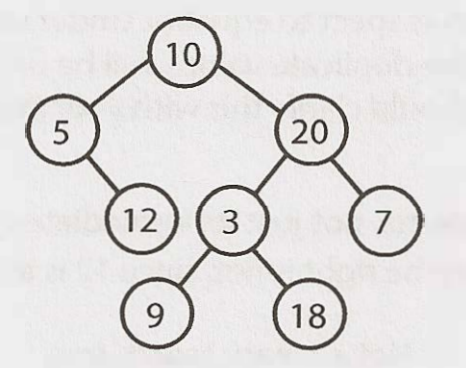
二元樹與二元搜尋樹 (Binary Tree vs. Binary Search Tree)

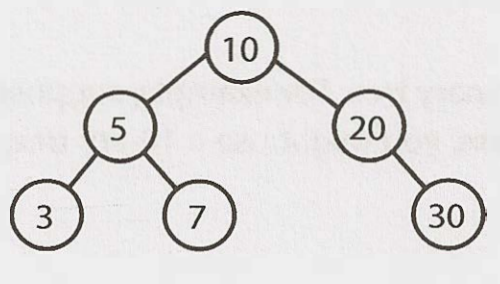
二元搜尋樹指每個節點都有特定排序的二元樹：
所有左邊 <= n < 所有右邊。此條件對每個節點n都成立。

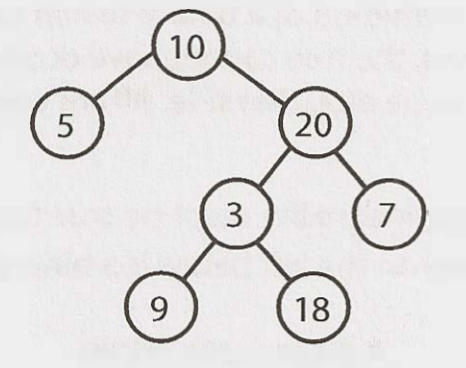
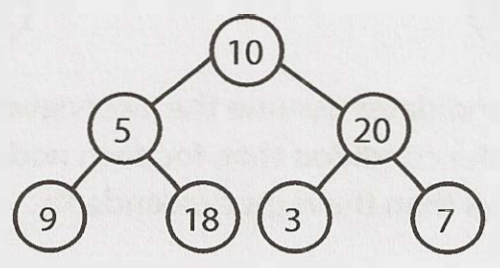
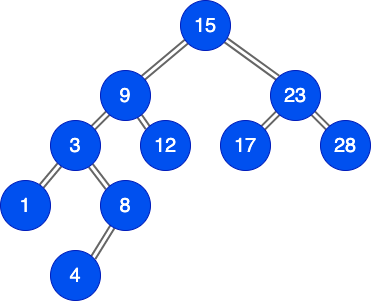
binary-search-tree
not-binary-search-tree

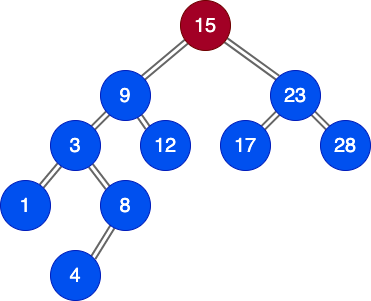
平衡與非平衡 (Balanced vs. Unbalanced)

注意平衡樹並不表示左右子樹大小完全相同。

實際意義是類似「未到糟糕等級的不平衡」。
它的平衡程度足以確保insert與find在$O(logn)$時間內。
(不一定要最佳平衡)

常見的平衡樹是紅黑樹(Red Black Tree)和AVL樹。

完全二元樹 (Complete Binary Trees)

指的是除了最後一層外，每層都填滿的二元樹。
最後一層從左至右填入。

not-complete-binary-tree
complete-binary-tree

滿二元樹 (Full Binary Trees)

指的是每個節點有零或兩個子節點的二元樹。
也就是說沒有節點只有一個子節點。

not-full-binary-tree
full-binary-tree

完美二元樹 (Perfect Binary Trees)

指的是所有葉節點均在同一層且葉具有最大節點數量。
剛好有$2^k-1$個節點。($k$為層數)

perfect-binary-tree

二元樹遍歷 (Binary Tree Traversal)

1
2
3
4
5
    4
   / \
  2   6
 / \ / \
1  3 5  7
遍歷方式 輸出結果
Pre-Order Traversal 4213657
In-Order Traversal 1234567
Post-Order Traversal 1325764

Pre-, In-, Post- 是指parent node相對於child node的順序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
<?php

class BinaryTreeNode
{
    public mixed $data;
    public ?BinaryTreeNode $left;
    public ?BinaryTreeNode $right;

    public function __construct($data)
    {
        $this->data = $data;
        $this->left = null;
        $this->right = null;
    }
}

前序遍歷 (Pre-Order Traversal)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
<?php

class PreOrder
{
  protected string $result = '';

  public function run(BinaryTreeNode $node): string
  {
    $this->preOrderTraversal($node);

    return $this->result;
  }

  public function preOrderTraversal(?BinaryTreeNode $node)
  {
    if ($node != null) {
      $this->visit($node);
      $this->preOrderTraversal($node->left);
      $this->preOrderTraversal($node->right);
    }
  }

  private function visit(BinaryTreeNode $node)
  {
    $this->result = $this->result . $node->data;
  }
}

中序遍歷 (In-Order Traversal)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
<?php

class InOrder
{
  protected string $result = '';

  public function run(BinaryTreeNode $node): string
  {
    $this->InOrderTraversal($node);

    return $this->result;
  }

  public function InOrderTraversal(?BinaryTreeNode $node)
  {
    if ($node != null) {
      $this->InOrderTraversal($node->left);
      $this->visit($node);
      $this->InOrderTraversal($node->right);
    }
  }

  private function visit(BinaryTreeNode $node)
  {
    $this->result = $this->result . $node->data;
  }
}

後序遍歷 (Post-Order Traversal)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
<?php

class PostOrder
{
  protected string $result = '';

  public function run(BinaryTreeNode $node): string
  {
    $this->PostOrderTraversal($node);

    return $this->result;
  }

  public function PostOrderTraversal(?BinaryTreeNode $node)
  {
    if ($node != null) {
      $this->PostOrderTraversal($node->left);
      $this->PostOrderTraversal($node->right);
      $this->visit($node);
    }
  }

  private function visit(BinaryTreeNode $node)
  {
    $this->result = $this->result . $node->data;
  }
}

二元堆積 - 最小堆積與最大堆積 (Binary Heaps - Min-Heaps and Max-Heaps)

最小堆積是個完全二元樹，其每個節點都小於子節點，
因此根是樹中的最小元素。

min-heap

有兩個關鍵操作：insert與extract_min。

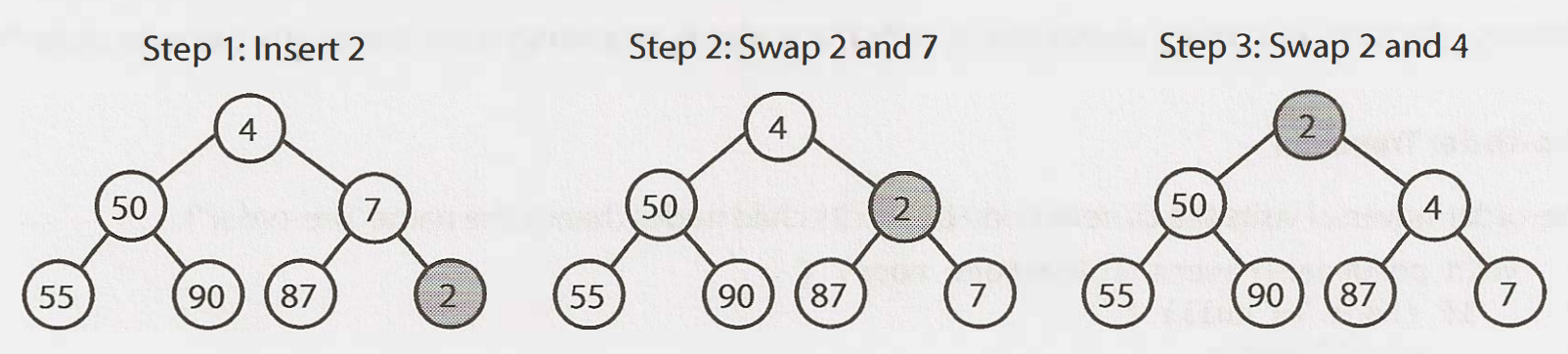
Insert

插入到最小堆積時，我們總是從底最右插入元素以維持完全樹。

然後我們改正樹，交換新元素與父元素直到新元素落在正確位置。
基本上就是將最小元素浮上去。

min-heap-insert

需要$O(logn)$時間，$n$為堆積的節點數量。

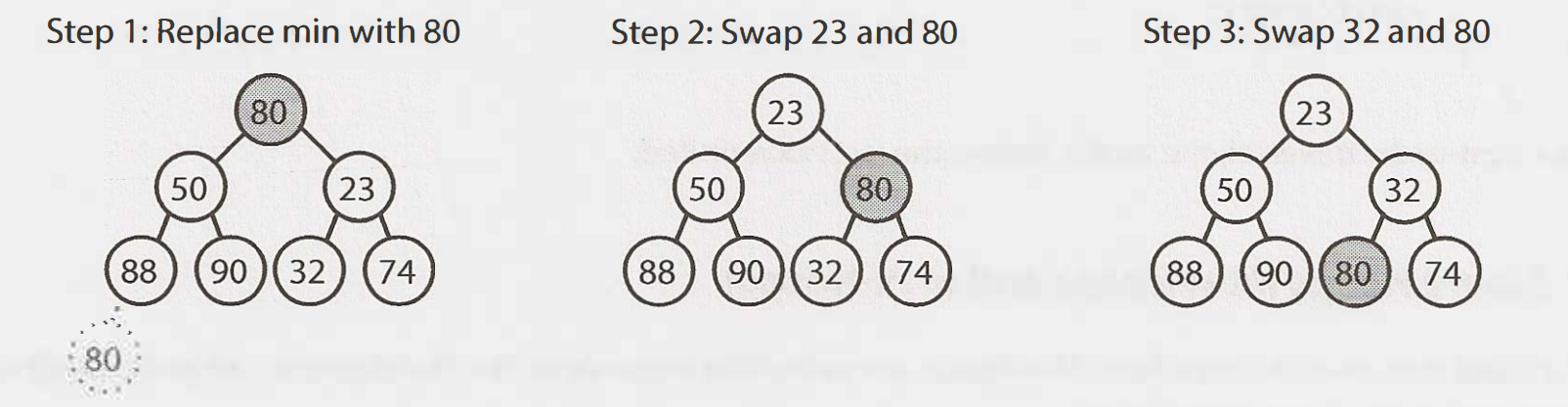
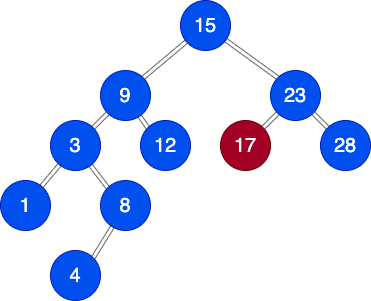
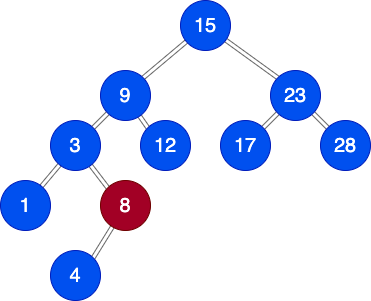
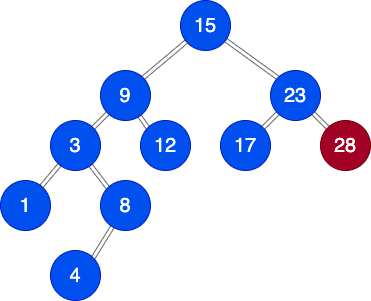
Extract Minimum Element

首先我們刪除最小元素並與堆積中最後一個元素(最下最右的元素)交換。
然後與子元素交換直到恢復成最小堆積。

與左或右的子元素交換？視其值而定。
左右元素間沒有自然的順序，但你必須取用較小者以維持最小堆積的順序。

min-heap-extract-minimum-element

(註: pdf版本的80並不符合最小堆積，書上的圖給的值是96)

此演算法也需要$O(logn)$時間。

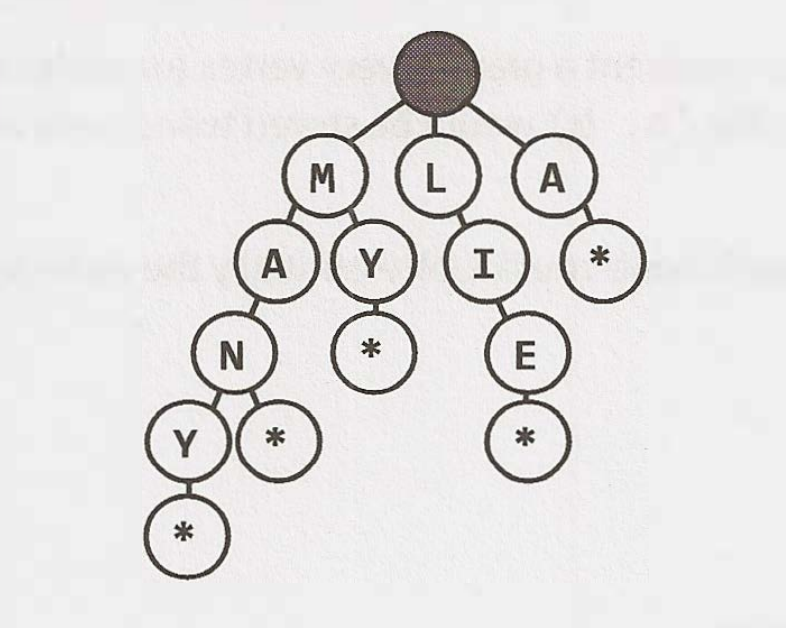
前綴樹 (Tries - Prefix Trees)

trie

前綴樹常用於儲存供前綴查詢的語言(英文)。

雖然雜湊表可以快速查詢某個字是否為合法的詞，
但無法告訴我們字串是否為前綴。
這點前綴樹可以做到。

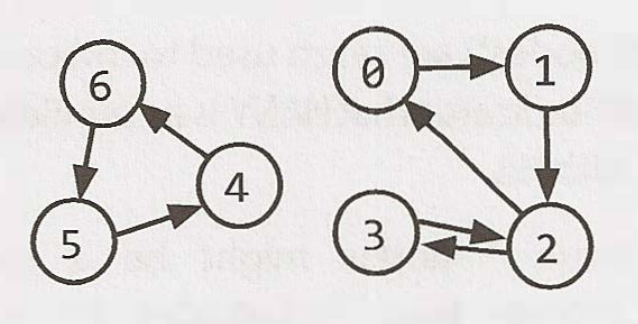
圖 (Graphs)

樹為圖的一種，但並非所有圖都是樹。

圖是群有邊 (edge) 的節點。

  • 圖可分有向 (directed) 或無向。
  • 圖可能由多個獨立的子圖組成。若每個點之間都有路徑連接則稱為「連通圖」(connected graph)。
  • 圖也可以有環。沒有環的圖稱為「無環圖」(acyclic graph)。

graph

通常有兩種常見的表示方式。

相鄰清單 (Adjacency List)

這是最常見的表示圖方式。
每個頂點 (vertex)(或稱為節點)儲存相鄰頂點的清單。
在無向圖中，(a, b)的邊會儲存兩次：
一次是a的相鄰頂點，一次是b的相鄰頂點。

1
2
3
4
5
6
7
8
9
10
11
<?php
class Graph
{
	public Node[] $nodes;
}

class Node
{
	public string $name;
	public Node[] $children;
}

此Graph類別是必要的，因為不像樹可從一個節點找到使用節點。

你不一定要額外的類別來表示圖。
上面的圖可表示為：
0: 1
1: 2
2: 0, 3
3: 2
4: 6
5: 4
6: 5

相鄰矩陣 (Adjacency Matrices)

相鄰矩陣是N*N布林矩陣 (N為節點數量)。
**matrix[i][j]**的true值表示節點i與節點j有邊。

在無向圖中，相鄰矩陣是對稱的。
在有向圖不一定對稱。

adjacency-matrices

圖搜尋 (Graph Search)

深度優先搜尋 (Depth-First Search, DFS)

在DFS中，我們造訪節點a然後迭代a的每個鄰居。
造訪a的鄰居b節點時，我們在進入a的其他鄰居前造訪b的所有鄰居。
也就是進入其他鄰居前完整搜尋b的分支。

注意前序與其他形式的樹遍歷也是一種DFS。
關鍵在於對圖實作時，我們必須檢查節點是否已經造訪過。

廣度優先搜尋 (Breadth-First Search, BFS)

在BFS中，節點a在造訪鄰居的鄰居前會造訪每一個鄰居。
你可以想像從a開始一層一層搜尋。
使用佇列的迭代方案通常最好。

用於找出來源與目標節點間的最短路徑。
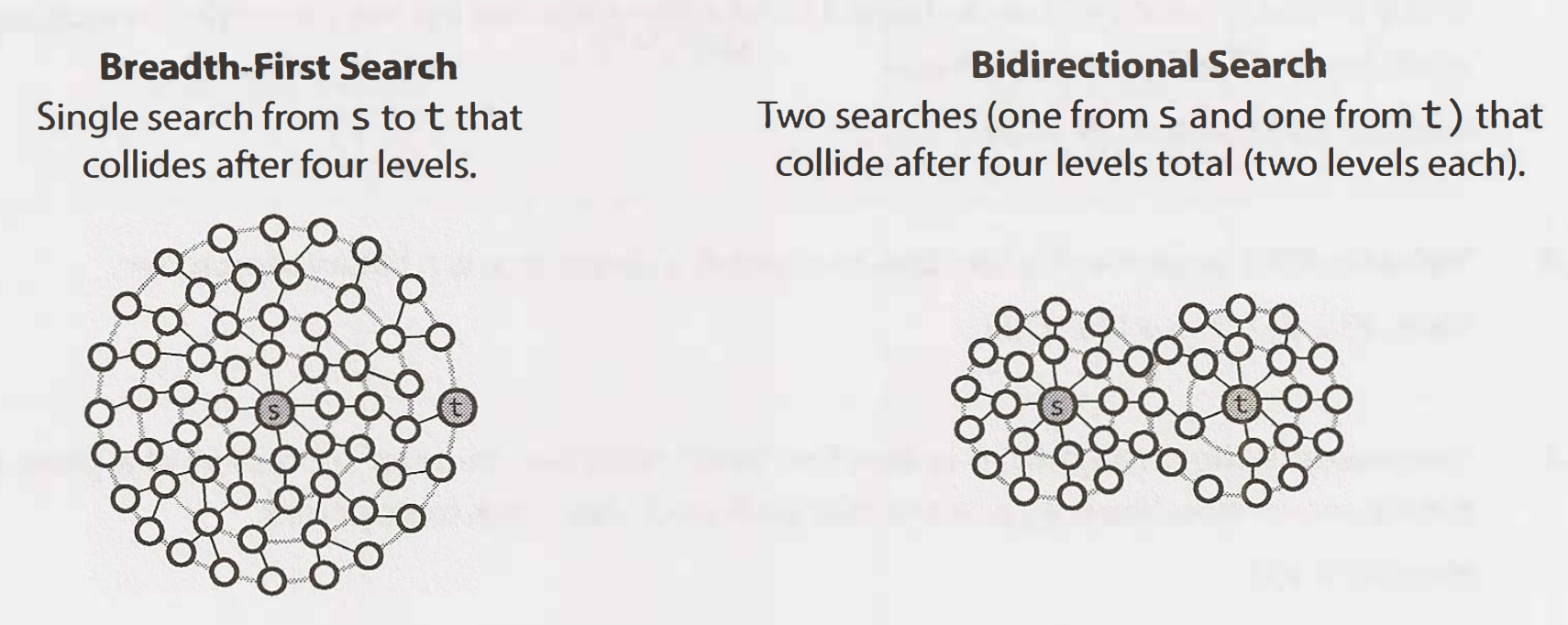
基本上是同時從兩個節點執行兩個廣度搜尋。

bidirectional-search

以每個節點最多有k個相鄰節點的圖來說，
從節點s到節點t的最短路徑長度為d。

  • 在廣度優先搜尋中，我們會在第一層搜尋最多$k$個節點。
    第二層對$k$個節點各搜尋$k$個節點，共有$k^2$個節點。
    會執行$d$次，因此有$O(k^d)$個節點。

  • 在雙向搜尋中，兩個搜尋約在$d/2$層後碰撞(路徑中點)。
    從s開始搜尋造訪約$O(k^{d/2})$次，從t開始也是。
    總共是$2*k^{d/2}$，或$O(k^{d/2})$個節點。

面試題目

  • Binary Tree Node
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
<?php

class BinaryTreeNode
{
    public mixed $data;
    public ?BinaryTreeNode $left;
    public ?BinaryTreeNode $right;

    public function __construct($data)
    {
        $this->data = $data;
        $this->left = null;
        $this->right = null;
    }
}

4.4 Check Balanced

Implement a function to check if a binary tree is balanced. For the purposes of this question, a balanced tree is defined to be a tree such that the heights of the two subtrees of any node never differ by more than one.

First Answer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
<?php

class BalancedTreeChecker
{
    public static function isBalanced(?BinaryTreeNode $node): bool
    {
        if (is_null($node)) {
            return true;
        }

        $heightDiff = abs(self::getHeight($node->left) - self::getHeight($node->right));

        if ($heightDiff > 1) {
            return false;
        } else {
            return self::isBalanced($node->left) && self::isBalanced($node->right);
        }
    }

    public static function getHeight(?BinaryTreeNode $node): int
    {
        if (is_null($node)) {
            return -1;
        }

        return max(self::getHeight($node->left), self::getHeight($node->right)) + 1;
    }

}

Second Answer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
<?php

class BalancedTreeChecker
{
    public static function isBalanced(?BinaryTreeNode $node): bool
    {
        if (is_null($node)) {
            return true;
        }

        return self::getHeight($node) != PHP_INT_MIN;
    }

    public static function getHeight(?BinaryTreeNode $node): int
    {
        if (is_null($node)) {
            return -1;
        }

        $leftHeight = self::getHeight($node->left);

        if ($leftHeight == PHP_INT_MIN) {
            return PHP_INT_MIN;
        }

        $rightHeight = self::getHeight($node->right);

        if ($rightHeight == PHP_INT_MIN) {
            return PHP_INT_MIN;
        }

        $heightDiff = abs($leftHeight - $rightHeight);

        if ($heightDiff > 1) {
            return PHP_INT_MIN;
        } else {
            return max($leftHeight, $rightHeight) + 1;
        }
    }

}

4.5 Validate BST

Implement a function to check if a binary tree is a binary search tree.

First Answer (In-Order Traversal)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
<?php

class BinarySearchTreeChecker
{
    protected static ?int $lastPrinted = null;

    public static function isBinarySearchTree(?BinaryTreeNode $node, $min = null, $max = null)
    {
        $result = self::checkBST($node);
        self::$lastPrinted = null;

        return $result;
    }

    public static function checkBST(?BinaryTreeNode $node)
    {
        if (is_null($node)) {
            return true;
        }

        if (!self::checkBST($node->left)) {
            return false;
        }

        if (!is_null(self::$lastPrinted) && $node->data < self::$lastPrinted) {
            return false;
        }

        self::$lastPrinted = $node->data;

        if (!self::checkBST($node->right)) {
            return false;
        }

        return true;
    }
}

4.6 Successor

binary-search-tree

Ideas:

  1. 若有右子樹，則是右子樹上最左邊的節點。

有右子樹的情況

  1. 若沒有右子樹，則要看節點與父節點的相對位置
    • 若節點在父節點的左邊，則下一個節點是父節點。

節點在父節點的左邊

  • 若節點在父節點的右邊，則下一個節點是父節點往上還沒遍歷的節點。
    即是下一個從左邊回去的節點。

節點在父節點的右邊

  1. 要小心若一路向上的過程中，沒有從左邊回去的節點。

沒有從左邊回去的節點

1
2
3
4
5
6
7
8
9
10
11
inorderSuccessor(Node n) {
  if (n has a right subtree) {
    return leftmost child of right subtree;
  } else {
    while (n.parent != null && n is a right child of n.parent) {
        n = n.parent;
    }

    return n.parent;
  }
}
  • Binary Tree Node With Parent
1
2
3
4
5
6
7
8
9
class BinaryTreeNodeWithParent extends BinaryTreeNode
{
    public $parent;

    public function __construct($data)
    {
        parent::__construct($data);
    }
}

First Answer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
<?php

class SuccessorNodeFinder
{
    private static function inorderSuccessor(?BinaryTreeNodeWithParent $node): ?BinaryTreeNode
    {
        if (is_null($node)) {
            return null;
        }

        if (!is_null($node->right)) {
            return self::leftMostChild($node->right);
        } else {
            $parent = $node->parent;

            while (!is_null($parent) && ($parent->left != $node)) {
                $node = $parent;
                $parent = $parent->parent;
            }

            return $parent;
        }
    }

    private static function leftMostChild(BinaryTreeNode $node): BinaryTreeNode
    {
        while (!is_null($node->left)) {
            $node = $node->left;
        }

        return $node;
    }


}

ʕ •ᴥ•ʔ：程式碼可參考：CtCI-6th-php。

Share