Algorithm

Math And Logic Puzzles

質數 (Prime Numbers)

每個正整數可以分解成質數的乘積。

例如：
$$84 = 2^2 * 3^1 * 5^0 * 7^1 * 11^0 * 13^0 * 17^0 * … $$

注意其中有很多質數的指數為0。

整除 (Divisibility)

若數字$x$整除數字$y$ ( 寫成 $x|y$ 或 $mod(y, x) = 0$ 或 $y≡0 (mod x)$ )，
則$x$所有的質因數必須在$y$的質因數中。

更精確的表示：
Let $x = 2^{j_0} * 3^{j_1} * 5^{j_2} * 7^{j_3} * 11^{j_4} * … $
Let $y = 2^{k_0} * 3^{k_1} * 5^{k_2} * 7^{k_3} * 11^{k_4} * … $
If $x|y,$ then $j_i <= k_i, ∀i∈N$

$x$與$y$的最大公因數是：
$$gcd(x, y) = 2^{min(j_0, k_0)} * 3^{min(j_1, k_1)} * 5^{min(j_2, k_2)} * …$$

$x$與$y$的最小公倍數是：
$$lcm(x, y) = 2^{max(j_0, k_0)} * 3^{max(j_1, k_1)} * 5^{max(j_2, k_2)} * …$$

思考一下$gcd * lcm$會得到什麼？

$gcd * lcm$
$= 2^{min(j_0, k_0)} * 2^{max(j_0, k_0)} * 3^{min(j_1, k_1)} * 3^{max(j_1, k_1)} * …$
$= 2^{min(j_0, k_0) + max(j_0, k_0)} * 3^{min(j_1, k_1) + max(j_1, k_1)} * …$
$= 2^{j_0 + k_0} * 3^{j_1 + k_1} * …$
$= 2^{j_0} * 2^{k_0} * 3^{j_1} * 3^{k_1}…$
$= xy$

檢查質數 (Checking for Primality)

從2迭代到$n-1$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
<?php

function primeNaive(int $n)
{
	if ($n < 2) {
		return false;
	}

	for ($i = 2; $i < $n; $i++) {
		if ($n % $i == 0) {
			return false;
		}
	}

	return true;
}

從2迭代到$n^{1/2}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
<?php

function primeNaive(int $n)
{
	if ($n < 2) {
		return false;
	}

	$sqrt = sqrt($n);

	for ($i = 2; $i < $sqrt; $i++) {
		if ($n % $i == 0) {
			return false;
		}
	}

	return true;
}

產生質數清單：埃拉托斯特尼篩法 (Generating a List of Primes: The Sieve of Eratosthenes)

利用所有非質數可被質數整除的概念來產生質數清單。

我們從最大值$max$的所有數字清單開始。

首先去掉可被2整除的數字，然後找出下個質數 (下個沒有被去掉的數字)，
並去掉可以被它整除的數字。
最終可以得到一個從2到$max$的質數清單。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
<?php

function sieveOfEratosthenes(int $maxNumber): array
{
	$numbers = range(2, $maxNumber);

	$prime = 2;
	while ($prime <= sqrt($maxNumber)) {
		$numbers = crossOff($numbers, $prime);

		$prime = getNextPrime($numbers, $prime);
	}

	return $numbers;
}

function crossOff(array $numbers, int $prime): array
{
	foreach ($numbers as $key => $number) {
		if ($number > $prime && $number % $prime == 0) {
			unset($numbers[$key]);
		}
	}

	return array_values($numbers);
}

function getNextPrime(array $numbers, int $prime): int
{
	foreach ($numbers as $key => $number) {
		if ($number > $prime) {
			return $number;
		}
	}

	return PHP_INT_MAX;
}

面試題目

6.1 The Heavy Pill

You have 20 bottles of pills. 19 bottles have 1.0 gram pills, but one has pills of weight 1.1 grams. Given a scale that provides an exact measurement, how would you find the heavy bottle? You can only use the scale once.

由於我們只能稱一次。
因此我們必須一次稱所有藥丸。

透過將瓶子編號，
從編號#1的瓶子取出1顆藥丸、
編號#2的瓶子取出2顆藥丸、…

我們會取出
$$1+2+3+…+20 = \frac{21*20}{2} = 210顆藥丸$$

若全為1克時，為210克。
超出的重量則來自1.1克的藥丸。

可透過以下公式找出瓶子編號：
$$\frac{weight - 210}{0.1}$$

6.2 Basketball

You have a basketball hoop and someone says that you can play one of two games. Game 1: You get one shot to make the hoop. Game 2: You get three shots and you have to make two of three shots. If p is the probability of making a particular shot, for which values of p should you pick one game or the other?

賭法一的勝率：p。

賭法二的勝率：

$P(賭法二)$
$= P(投三中三) + P(投三中二)$
$= p * p * p + p * p * (1-p) * 3$
$= p^3 + 3p^2(1-p)$

要選哪一種玩法?

考慮
$p > p^3 + 3p^2(1-p)$
$2p^3 - 3p^2 + p > 0$
$2p^2 - 3p + 1 > 0$
$(2p-1)(p-1) > 0$

得$0 < p < \frac{1}{2}$

故
(i) 當$0 < p < \frac{1}{2}$選賭法一。
(ii) 當$0.5 < p < 1$選賭法二。
(iii) 當$p = 0$、$p = 0.5$、$p = 1$時則都可以。

6.3 Dominos

There is an 8x8 chessboard in which two diagonally opposite corners have been cut off. You are given 31 dominos, and a single domino can cover exactly two squares. Can you use the 31 dominos to cover the entire board? Prove your answer (by providing an example or showing why it’s impossible).

6.4 Ants on a Triangle

There are three ants on different vertices of a triangle. What is the probability of collision (between any two or all of them) if they start walking on the sides of the triangle? Assume that each ant randomly picks a direction, with either direction being equally likely to be chosen, and that they walk at the same speed. Similarly, find the probability of collision with n ants on an n-vertex polygon.

不碰撞的情況比較單純。

情況一：全部都走順時針的機率

$\frac{1}{2} * \frac{1}{2} * \frac{1}{2} = \frac{1}{8}$

情況二：全部都走逆時針的機率

$\frac{1}{2} * \frac{1}{2} * \frac{1}{2} = \frac{1}{8}$

則碰撞機率
$1 - \frac{1}{8} * 2 = \frac{6}{8} = \frac{3}{4}$

通用情況：$n$隻螞蟻在$n$邊形的碰撞機率

$1 - (\frac{1}{2})^n * 2$

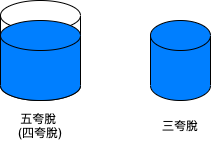
6.5 Jugs of Water

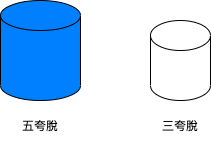
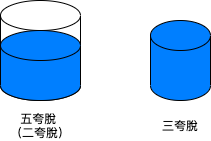
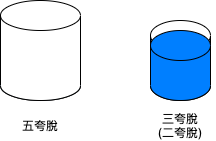
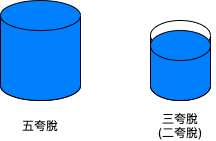
You have a five-quart jug, a three-quart jug, and an unlimited supply of water (but no measuring cups). How would you come up with exactly four quarts of water? Note that the jugs are oddly shaped, such that filling up exactly “half” of the jug would be impossible.

透過五夸脫與三夸脫的容積差。

step1
step2
step3
step4
step5

6.6 Blue-Eyed Island

A bunch of people are living on an island, when a visitor comes with a strange order: all blue-eyed people must leave the island as soon as possible. There will be a flight out at 8:00 pm every evening. Each person can see everyone else’s eye color, but they do not know their own (nor is anyone allowed to tell them). Additionally, they do not know how many people have blue eyes, although they do know that at least one person does. How many days will it take the blue-eyed people to leave?

情況一：假設一個藍眼人
在他眼中沒有其他藍眼人，他就會知道自己是唯一的藍眼人。

費時一天。

情況二：假設兩個藍眼人

在他們眼中有一個藍眼人，
過了一晚，發現該藍眼人沒有離開。

這表示那個藍眼人中還有藍眼人，
即自己也是藍眼人。

費時兩天。

依次推類

若有$n$個聰明的藍眼人，則費時$n$天。

ʕ •ᴥ•ʔ：程式碼可參考：CtCI-6th-php。