460.lfu-cache

Description:

Design and implement a data structure for a Least Frequently Used (LFU) cache.

Implement the LFUCache class:

• LFUCache(int capacity) Initializes the object with the capacity of the data structure.
• int get(int key) Gets the value of the key if the key exists in the cache. Otherwise, returns -1.
• void put(int key, int value) Update the value of the key if present, or inserts the key if not already present. When the cache reaches its capacity, it should invalidate and remove the least frequently used key before inserting a new item. For this problem, when there is a tie (i.e., two or more keys with the same frequency), the least recently used key would be invalidated.

To determine the least frequently used key, a use counter is maintained for each key in the cache. The key with the smallest use counter is the least frequently used key.

When a key is first inserted into the cache, its use counter is set to 1 (due to the put operation). The use counter for a key in the cache is incremented either a get or put operation is called on it.

The functions get and put must each run in O(1) average time complexity.

Example 1:

Input
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
Output
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]

Explanation
// cnt(x) = the use counter for key x
// cache=[] will show the last used order for tiebreakers (leftmost element is  most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1);   // cache=[1,_], cnt(1)=1
lfu.put(2, 2);   // cache=[2,1], cnt(2)=1, cnt(1)=1
lfu.get(1);      // return 1
                 // cache=[1,2], cnt(2)=1, cnt(1)=2
lfu.put(3, 3);   // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
                 // cache=[3,1], cnt(3)=1, cnt(1)=2
lfu.get(2);      // return -1 (not found)
lfu.get(3);      // return 3
                 // cache=[3,1], cnt(3)=2, cnt(1)=2
lfu.put(4, 4);   // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
                 // cache=[4,3], cnt(4)=1, cnt(3)=2
lfu.get(1);      // return -1 (not found)
lfu.get(3);      // return 3
                 // cache=[3,4], cnt(4)=1, cnt(3)=3
lfu.get(4);      // return 4
                 // cache=[4,3], cnt(4)=2, cnt(3)=3

Constraints:

• 0 <= capacity <= $10^4$
• 0 <= key <= $10^5$
• 0 <= value <= $10^9$
• At most $2 * 10^5$ calls will be made to get and put.

---

Double Linked List (with sentinel node)

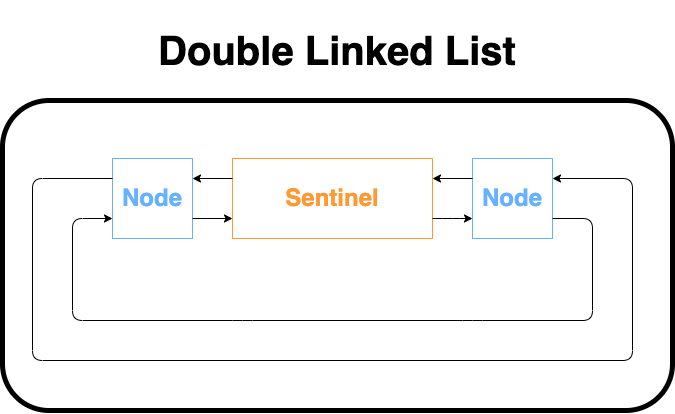
優點：
透過設置sentinel，可以快速取得第一個節點和最後一個節點。

---

Appropriate Answer (Double Linked List):

<?php

namespace LeetCode\LFUCache;

class Node
{
    public ?int $key;
    public ?int $value;
    public int $frequence;
    public ?Node $prev;
    public ?Node $next;

    public function __construct(
        ?int $key,
        ?int $value
    ) {
        $this->key = $key;
        $this->value = $value;

        $this->frequence = 1;
        $this->prev = null;
        $this->next = null;
    }
}

class DoubleLinkedList
{
    public Node $sentinel;
    public int $size;

    public function __construct()
    {
        $this->sentinel = new Node(null, null);
        $this->sentinel->next = $this->sentinel;
        $this->sentinel->prev = $this->sentinel;

        $this->size = 0;
    }

    public function append(Node $node)
    {
        $node->prev = $this->sentinel;
        $node->next = $this->sentinel->next;

        $this->sentinel->next->prev = $node;
        $this->sentinel->next = $node;

        $this->size++;
    }

    public function pop(?Node $node = null): ?Node
    {
        if ($this->size == 0) {
            return null;
        }

        //good thinking
        if (is_null($node)) {
            $node = $this->sentinel->prev;
        }

        $node->prev->next = $node->next;
        $node->next->prev = $node->prev;

        $this->size--;

        return $node;
    }
}

class LFUCache
{
    public int $capacity;
    public int $size;
    public array $nodeDictionary;
    public array $doubleLinkedListCollection;
    public int $minFrequence;

    const NODE_NOT_EXISTS = -1;

    /**
     * @param int $capacity
     */
    public function __construct($capacity)
    {
        $this->capacity = $capacity;
        $this->size = 0;
        $this->nodeDictionary = [];
        $this->doubleLinkedListCollection = [];
        $this->minFrequence = 0;
    }

    /**
     * @param int $key
     * @return int
     */
    public function get($key)
    {
        if (!isset($this->nodeDictionary[$key])) {
            return self::NODE_NOT_EXISTS;
        }

        $node = $this->nodeDictionary[$key];
        $frequence = $node->frequence;

        $doubleLinkedList = $this->doubleLinkedListCollection[$frequence];
        $doubleLinkedList->pop($node);

        if ($doubleLinkedList->size == 0 && $frequence == $this->minFrequence) {
            $this->minFrequence++;
        }

        $node->frequence++;
        $frequence = $node->frequence;

        if (!isset($this->doubleLinkedListCollection[$frequence])) {
            $this->doubleLinkedListCollection[$frequence] = new DoubleLinkedList();
        }

        $doubleLinkedList = $this->doubleLinkedListCollection[$frequence];
        $doubleLinkedList->append($node);

        return $node->value;
    }

    /**
     * @param int $key
     * @param int $value
     * @return void
     */
    public function put($key, $value): void
    {
        if ($this->capacity == 0) {
            return;
        }

        if (isset($this->nodeDictionary[$key])) {
            $node = $this->nodeDictionary[$key];
            $node->value = $value;
            $frequence = $node->frequence;

            $doubleLinkedList = $this->doubleLinkedListCollection[$frequence];
            $doubleLinkedList->pop($node);

            if ($doubleLinkedList->size == 0 && $frequence == $this->minFrequence) {
                $this->minFrequence++;
            }

            $node->frequence++;
            $frequence = $node->frequence;

            if (!isset($this->doubleLinkedListCollection[$frequence])) {
                $this->doubleLinkedListCollection[$frequence] = new DoubleLinkedList();
            }

            $doubleLinkedList = $this->doubleLinkedListCollection[$frequence];
            $doubleLinkedList->append($node);

            return;
        }

        if ($this->size == $this->capacity) {
            $doubleLinkedList = $this->doubleLinkedListCollection[$this->minFrequence];
            $unsetNode = $doubleLinkedList->pop();

            $unsetNodeKey = $unsetNode->key;
            unset($this->nodeDictionary[$unsetNodeKey]);

            $this->size--;

            if ($doubleLinkedList->size == 0 && $this->minFrequence > 0) {
                $this->minFrequence--;
            }
        }

        $node = new Node($key, $value);
        $this->nodeDictionary[$key] = $node;

        if (!isset($this->doubleLinkedListCollection[1])) {
            $this->doubleLinkedListCollection[1] = new DoubleLinkedList();
        }

        $doubleLinkedList = $this->doubleLinkedListCollection[1];
        $doubleLinkedList->append($node);

        $this->minFrequence = 1;
        $this->size++;
    }
}

• Time Complexity: $O(1)$

---

(Reference.)

• Python concise solution detailed explanation: Two dict + Doubly linked list

---

ʕ •ᴥ•ʔ：這題難度hard，看完討論還是弄了好久好久。
有小瑕疵時，第21個test case不好debug。