Programming

Big O

Big O是用來評估演算法效能的一種方式。

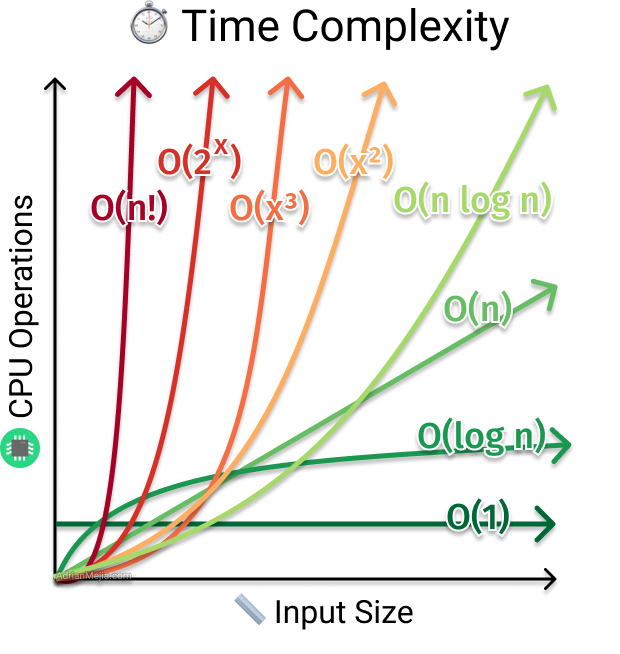
時間複雜性

Big O、Big Theta、與Big Omega

  • O (Big O):描述時間上限。
  • Ω (Big omega):描述時間下限。
  • Θ (Big theta):同時表示O與Ω。

通常面試時講的Big O，比較接近學術界的Θ。

最佳情況、最差情況、與預期情況

我們將以 快速排序法 (Quick Sort) 為例。

補充:
快速排序法的原理是先從原始資料中找一個基準值(Pivot)，
接著逐一將資料與基準值比較，小於基準值的資料放在左邊，大於基準值的資料放在右邊，
再將兩邊區塊分別再找出基準值，重複前面的步驟，直到排序完為止。

使用分治法(Divide and Conquer)的概念。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 原始資料
40 60 50 20 10 30

// 選擇最左邊的資料為基準點
[40] 60 50 20 10 30

// 60 > 40，要移到40的右邊
[40] 60 50 20 10 30
     ^

// 50 > 40，要移到40的右邊
[40] 60 50 20 10 30
        ^

// 20 < 40，要移到40的左邊
[40] 60 50 20 10 30
           ^
20 [40] 60 50 10 30

// 10 < 40，要移到40的左邊
20 [40] 60 50 10 30
              ^
20 10 [40] 60 50 30

// 同理30 < 40，要移到40的左邊
20 10 [40] 60 50 30
                 ^
20 10 30 [40] 60 50

// 第一次排序完成
20 10 30 40 60 50

// 接著排序40左右兩側的資料
// 先排左側資料，同樣選擇最左邊的資料為基準點
// 左側基準點為20
[20] 10 30 40 60 50

// 左側資料排序完成
10 [20] 30 40 60 50

// 接著排序右側資料，一樣選擇最左邊的資料為基準點
// 右側基準點為60
10 20 30 40 [60] 50

//右側排序完成
10 20 30 40 50 [60]

//排序結果
10 20 30 40 50 60
  • 最佳情況: 若所有元素相等，則快速排序法平均只會遍歷一次，執行時間為$O(N)$。
  • 最差情況: 若很不幸地，每次基準點都選到最大元素，則執行時間為$O(N^2)$。
  • 預期情況: 通常不會是最佳情況或最差情況，所以執行時間為$O(nlog{n})$。

空間複雜度

空間複雜性與時間複雜性是平行的概念。
若建構大小為n的陣列，它需要$O(n)$空間。
若需要nxn的二維陣列，則需要$O(n^2)$空間。

遞迴呼叫所需的堆疊(stack)空間也是。

1
2
3
4
5
6
int sum(int n) {
  if (n <= 0) {
    return 0;
  }
  return n + sum(n - 1);
}

每個呼叫增加了堆疊層級。

1
2
3
4
5
sum(4)
  -> sum(3)
    ->sum(2)
      ->sum(1)
        ->sum(0)

但有n個呼叫，不表示佔用$O(n)$空間。

1
2
3
4
5
6
7
8
9
10
11
int pairSumSequence(int n) {
  int sum = 0;
  for (int i = 0; i < n; i++) {
    sum += pairSum(i, i+1);
  }
  return sum;
}

int pairSum(int a, int b) {
  return a + b;
}

有$O(n)$個對pairSum的呼叫，但這些呼叫不同時存在堆疊，
因此只需要$O(1)$的空間。

降低常數

1
2
3
4
5
6
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int x : array) {
  if (x < min) min = x;
  if (x > max) max = x;
}
1
2
3
4
5
6
7
8
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int x : array) {
  if (x < min) min = x;
}
for (int x : array) {
  if (x > max) max = x;
}

許多人會視第二個for迴圈為$O(2N)$，認為這樣比較“精確”。並不是。

在Big O判斷執行時間如何放大時，我們只需接受$O(N)$一定比$O(N^2)$好。

降低非優勢條件

  • $O(N^2 + N)$變成$O(N^2)$
  • $O(N + log{N})$變成$O(N)$
  • $O(5*2^N + 1000N^{100} )$變成$O(2^N)$

然而執行時間還是可能有加總。例如$O(B^2 + A)$。

常見Big O時間的增加速率

多部份演算法：加與乘

  • 執行時間相加: $O(A + B)$

    1
    2
    3
    4
    5
    6
    for (int a : arrA) {
      print(a);
    }
    for (int b : arrB) {
      print(b);
    }

  • 執行時間相加: $O(A * B)$

    1
    2
    3
    4
    5
    for (int a : arrA) {
      for (int b : arrB) {
        print(a + "," + b);
      }
    }

若演算法形式為“做這個，完成後，做那個”，則執行時間相加。
若演算法形式為“每次做這個時要做那個”，則執行時間相乘。

平攤時間

ArrayList或動態調整大小的陣列兼具陣列功能與彈性大小。
遇到上限時，會建構兩倍大小的新陣列並複製所有元素到新陣列中。

那麼你要如何描述插入的執行時間？

陣列滿的情況(假設有N個元素)，則插入新元素要$O(N)$時間。
你必須先建構大小2N的新陣列，然後複製N個元素。

但我們知道它不常發生。大部分的插入時間為$O(1)$時間。

我們將考慮平攤(amortized)時間。

插入元素將加倍容量，因此在X個元素的情況。
我們將經歷 $1 + 2 + 4 + … + X$ 個複製。

反過來看，就是 $X + X/2 + X/4 + … + 1$。約為2X。
(無限等比級數)

因此X個插入，需要$O(2X)$時間。
每個插入的平攤時間為$O(1)$。

log N 執行時間

當你看到題目中元素的數量每次折半，它很可能就是$O(log{n})$執行時間。

遞迴執行時間

下列這段程式碼的執行時間是？

1
2
3
4
5
6
int f(int n) {
  if (n <= 1) {
    return 1;
  }
  return f(n-1) + f(n-1);
}

假設呼叫f(4)

1
2
3
4
5
6
7
                               f(4)

                f(3)                            f(3)

       f(2)             f(2)            f(2)              f(2)

f(1)        f(1)  f(1)        f(1) f(1)       f(1)   f(1)         f(1)

這個樹有幾個呼叫？ (不要一個一個數！)

這個樹的深度為N。每個節點 (也就是函式呼叫)有兩個子節點。
因此每一層比前一層多一倍呼叫。

層 # 節點數量 也表示為… 或…
0 1 $2^0$
1 2 2 * 前一層 = 2 $2^1$
2 4 2 * 前一層 = 2 * $2^1$ = $2^2$ $2^2$

共有 $2^0 + 2^1 + … + 2^N $ 也就是 $2^{N+1}-1$ 個節點。

嘗試記住這個表。
遇到多次呼叫的遞迴函式時，執行時間通常 (但不一定) 會是 $O(分支^{深度})$，
分支為每個遞迴呼叫再呼叫的數量。

此演算法空間複雜度為$O(N)$。
雖然樹節點總數為$O(2^N)$，任一時間只有出現$O(N)$個。

f(n), f(n-1), …, f(1)

因此只需要$O(N)$記憶體空間。

範例與練習

範例12

此程式計算字串的排列。
請問它的時間複雜度是？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void permutation(String str) {
  permutation(str, "");
}

void permutation(String str, String prefix) {
  if (str.length() == 0) {
    System.out.println(prefix);
  } else {
    for (int i = 0; i < str.length(); i++) {
      String rem = str.substring(0, i) + str.substring(i + 1);
      permutation(rem, prefix + str.charAt(i));
    }
  }
}

Q1. permutation有多少次終止條件呼叫？

$n*(n-1)*…*1 = n!$ 次的呼叫。

Q2. permutation有多少次終止條件前呼叫？
考慮程式碼第9~12行跑幾次。

1
2
3
4
     abc
 a    b    c
b c  a c  a b
c b  c a  b a

想像有$n!$個葉，每個葉連結長$n$的路徑。
所以不會有超過$n*(n-1)!$個節點。

因此Q1 + Q2共有 $n*n!$ 個節點。

Q3. 每個呼叫要花多久？

第7行輸出$n$個字元，需要$O(n)$時間。
第10,11行，因為字串連接 (rem, prefix與str.charAt(i)加總長度為n)
故為$O(n)$時間。

Q4. 總執行時間？
$$ n * n! * n = O(n^2*n!) $$

ʕ •ᴥ•ʔ：這題感覺只能求最接近解。

範例16

下列函式輸出從1到n(含)的2冪。
舉例來說，若n為4，它會輸出1、2與4。其執行時間是？

1
2
3
4
5
6
7
8
9
10
11
12
13
int powersOf2(int n) {
  if (n < 1) {
    return 0;
  } else if (n == 1) {
    System.out.println(1);
    return 1;
  } else {
    int prev = powersOf2(n/2);
    int curr = prev * 2;
    System.out.println(curr);
    return curr;
  }
}

可以看出執行時間是$O(log_n)$。

這邊有另一種思考方式是思考隨著$n$增加時執行時間如何變化。

何時 powersOf2 的呼叫次數會增加？

每次 $n$ 加倍大小時會加1。

VI.2

下列程式計算$a^b$。執行時間是？

1
2
3
4
5
6
7
8
9
int power(int a, int b) {
  if (b < 0) {
    return 0; //錯誤
  } else if (b == 0) {
    return 1;
  } else {
    return a * power(a, b - 1);
  }
}

會由b依序減1呼叫到0，故$O(b)$。

VI.5

下列程式計算整數平方根。
若數字非完美平方 (沒有整數平方根)則回傳 -1。

執行時間是？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int sqrt(int n) {
  return sqrt_helper(n, 1, n);
}

int sqrt_helper(int n, int min, int max) {
  if (max < min) return -1;

  int guess = (min + max) / 2;

  if (guess *guess == n) {
    return guess;
  } else if (guess * guess < n) {
    return sqrt_helper(n, guess + 1, max);
  } else {
    return sqrt_helper(n, min, guess - l);
  }
}

ʕ •ᴥ•ʔ：原本以為會是 $O(\sqrt{n})$。
但觀察上面第八行，會知道每次減半，故為 $O(log(n))$。

VI.6

同上題，求程式計算整數平方根。

執行時間是？

1
2
3
4
5
6
7
8
9
int sqrt(int n) {
  for (int guess = 1; guess * guess <= n; guess++) {
    if (guess * guess == n) {
      return guess;
    }
  }

  return -1;
}

這題就是$O(\sqrt{n})$了。

VI.8

從二元樹查詢特地資料，但其非二元搜尋樹。

執行時間是？

Note.

  1. 二元樹(Binary tree)是每個節點最多只有兩個分支的樹結構。

  2. 二元搜尋樹(Binary Search Tree)，
    又稱有序二元樹(ordered binary tree)或排序二元樹(sorted binary tree)。

是空樹或有以下幾個特點的二元樹:

  • 若任意節點的左子樹不空，則左子樹上所有節點的值均小於它的根節點的值
  • 若任意節點的右子樹不空，則右子樹上所有節點的值均大於它的根節點的值
  • 任意節點的左、右子樹也分別為二元搜尋樹

由定義，節點可能沒有排序，故為 $O(n)$。

VI.11

下列程式輸出字元排序過長度為k的所有字串。
它產生所有k長度字串，然後檢查是否有排序。

執行時間是？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int numChars = 26;

void printSortedStrings(int remaining) {
  printSortedStrings(remaining, "");
}

void printSortedStrings(int remaining, String prefix) {
  if (remaining== 0) {
    if (isinOrder(prefix)) {
      System.out.println(prefix);
    }
  } else {
    for (int i= 0; i < numchars; i++) {
      char c = ithletter(i);
      printSortedStrings(remaining - 1, prefix + c);
  }
}

boolean isinOrder(String s) {
  for (int i= 1; i < s.length(); i++) {
    int prev ithLetter(s.charAt(i - 1));
    int curr = ithLetter(s.charAt(i));

    if (prev > curr) {
      return false;
    }
  }
  return true;
}

char ithLetter(int i) {
  return (char) (((int) 'a') + i);
}

(參考stackoverflow)

The above algorithm works by recursively generating all possible strings of length k using a set of c choices of characters. The number of possible strings of length k you can make from c choices of letters is equal to $c^k$.

  • ithLetter 執行時間為$O(1)$。
  • isinOrder 執行時間為$O(k)$。
  • printSortedStrings 這邊則是選擇長度k，再從字母字元數量c中，依次挑選字母。
    單看挑選字母的執行時間為$O(c^k)$。而我們會根據長度k，遞迴地呼叫。
    因此執行時間為$O(k\times{c^k})$。

References:

ʕ •ᴥ•ʔ：在讀重構extract method，將一個迴圈的多種職責，分開到多個迴圈時，
Kyo曾提出很好的比喻：abab跟aabb的效率是相同的。
即是降低常數的概念。

Share